Поиск среди миллиарда слов. Считаем количество N-Gram.

В прошлом посте я обещал расшарить результаты своего ночного кодинга, так что это вроде как продолжение (практическая часть). Здесь уже будет технический хардкор на Java.

Оцениваем сложность по пямяти

Для начала надо было придумать как посчитать сколько раз встречаютсы все эти "the", "the cat", "the cat likes" и т.д. Уникальных слов будет много, а уникальных bi-,tri-, и.т.д -gramm будет еще больше. Для каждой n-gramm'ы нужно хранить сколько раз она встречается в тексте. Чтобы примерно оценить масштаб проблемы я предварительно спросил у гугла "сколько слов в английском языке?"
Гугл говорит, что более 1млн:

Если считать только количество unigram (уникальных слов), то это не проблема хранить 1млн счетчиков в памяти, но как только понядобятся 2-,3-..грамы, то требования к памяти совсем другие. Для bigram в худшем случае понадобится хранить \(1млн^2\) каунтеров, для trigram \(1млн^3\) и т.д.
Хотелось бы обойтись без всяких DB/NoSQL и прочих Hadoop'ов, поскольку это сильно утяжелит решение. Я начну с чего-то простого, но достаточно эффективного по памяти.

Структура данных Trie

Попробую использовать структуру данных Trie (хороший пример можно также посмотреть здесь). В моем случае Trie будет все тем же деревом, где каждый узел представляет слово, а дочки-возможные варианты слов, которые следуют за ним.

Поясню на примере.
Возьмем предложения "The dog likes the cat" и "the cat hates the dog".
Вот как будет выглядеть Trie после того, как посчитаю количество биграм для этих 2х предложений:

По дереву легко можно найти, например, что слово "the" встречается 4 раза, а "the dog" - 1 раз. Слово "dog" - 2 раза, а "dog likes" - 1 и т.д. При увеличении "N-грамности" дерево будет содержать новые уровни. Количество уровней в trie будет равно числу N в N-Gram'е (рутовую ноду я не считаю). 

Пишу код

Сам код здесь не буду постить, для этого есть гитхаб:https://github.com/szelenin/kaggle/tree/master/billion-word-imputation. Укажу лишь, что но начал я с такого теста:

А закончил таким:

Все слова приводятся к нижнему регистру, знаки препинания и прочие нетерминальные символы я решил отбросить.

Пробный пуск

Для начала я запустил подсчет уникальных слов, чтобы получить общую статистику по тренировочному файлу. Вот что выдала после 2х с небольшим минут.

Lines read: 30301028. Unique words: 1026207, total words: 693467918

Количество уникальных слов практически такое же как выдал гугл. Так что, думаю, все возможные слова, которые есть в английском языке присутствуют :)

1й запуск для подсчета триграм

Я особенно не расчитывал, что моя считалка посчитает количество всех возможных триграм в тексте, просто интересно через сколько времени закончится память :). Память закончилась практически сразу и JVM вывалился с жуткой ошибкой:

# A fatal error has been detected by the Java Runtime Environment:

#

#  EXCEPTION_ACCESS_VIOLATION (0xc0000005) at pc=0x000000006f533c0b, pid=4768, tid=6776

#

# JRE version: Java(TM) SE Runtime Environment (8.0_20-b26) (build 1.8.0_20-b26)

2й запуск

На второй запуск я выделил 12Гб под JVM и запустил jvisualvm чтобы посмотреть как кушается память. Проработала программка 4минуты и вывалилась с такой же ошибкой. Но все таки успела  прочитать 3.6 млн строк, в которых было 83.5 млн слов, из которых почти 400 тыс уникальных, что в общем-то неплохо для 4х минут работы :) :

Lines read: 3648300. Unique words: 398484, total words: 83500620

Вот как заполнялась память

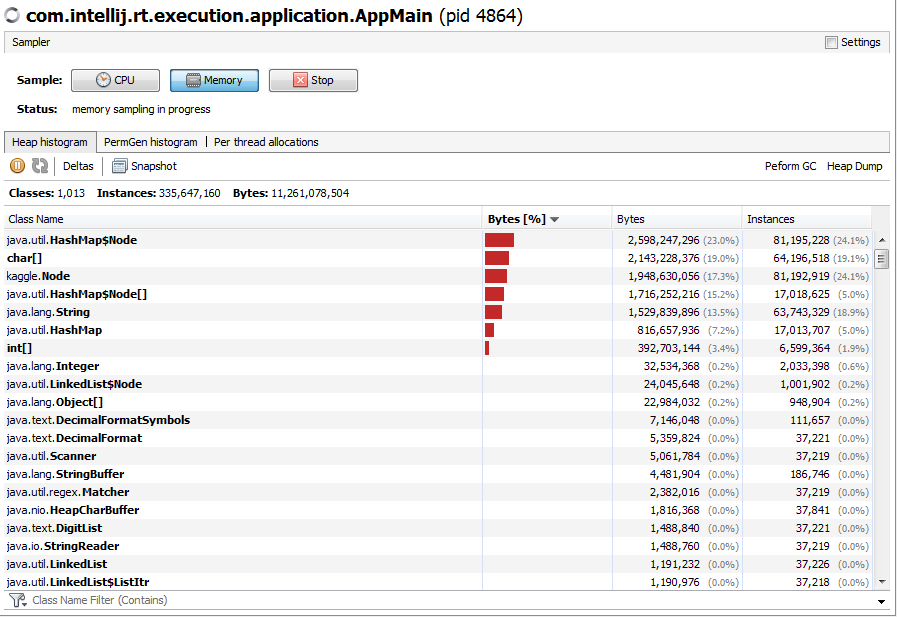
 А вот какие обьекты наиболее активно ее наполняли:

Глядя на количество инстансов HashMap я решил немного сэкономить и чуть оптимизировать код. Дело в том, что в каждой ноде я по умолчанию создавал мапу для ее детей:

Но для последнего уровня дерева детей не предполагается, поэтому можно мапу не создавать.

3й запуск

Сделал создание мапы с детьми lazy и запустил еще раз. На этот раз работало 30 минут, после чего я убил процесс, т.к. дожидаться правильного OutOfMemory совсем не хотелось. Перед смертью считалка отчиталась, что прочитала 7.1 млн предложений из 16.2млн слов, из которых 541тыс уникальных.

Lines read: 7119000. Unique words: 541538, total words: 162929078

Вот график поедания памяти

 А вот ее содержимое

Выводы

Считалка свободно просчитывает 4млн предложений за 4минуты. В тренировочном наборе всего 30млн. Можно, конечно, придумывать новые способы хранения счетчиков, подключать внешние хранилища данных, и т.д. но это может превратиться в бесконечный процесс. Хотелось бы закончить с начальной версии модели, а затем ее усовершенствовать в плане производительности. Поэтому я разобью тренировочный набор на 10 частей и буду работать с ними отдельно. Еще надо найти где пропущено слово и, самое сложное, какое слово вместо него нужно добавить. Так что буду отлаживать модель на одном из 10 наборов или на каждом по очереди, а затем будем думать как обьеденить.

PS

Как говорится "быстро сказка сказывается, но не быстро дело делается". На следующий день я бодренько поправил код, который разбивает тренировочный набор на 10 частей, считает каунтеры и сохраняет расчитанные значения в файле. Запустил прогу и через 30 минут она вывалилась с таким же ACCESS VIOLATION как и в 1й раз. Вот так съедалась память во время работы:

Это довольно странно, т.к. после каждой просчитанной порции тренировочного файла GC должен был убрать все что с этой порцией связано. Так что я ожидал увидеть несколько "холмов" в графике. 

Ради эксперимента я сказал JVM использовать Garbage Collector GC1 (-XX:+UseG1GC) и запустил считалку опять. На этот раз она упала при сериализации модели, так что я поменял стандартную Java сериализацию на kryo и запустил еще раз. В этот раз все прошло как и ожидалось:

График показывает, что GC корректно убивает ненужные объекты. Тогда почему это не работало раньше, с Garbage collector'ом, по умолчанию? 

По умолчанию применяется Concurrent Mark&Sweep GC, который разделяет объекты на "короткоживущие" и "долгоживущие". Область короткоживущих чистится часто, а долгоживущие чистятся гораздо реже. Если JVM положил объект в "долгоживущую" область, то потом его оттуда сложно будет вытащить. По крайней мере в моем случае похоже, что все попытки почистить долгоживущую область заканчивались крашем JVM. GC1 разделяет весь хип на блоки размером от 1 до 32мб. Каждый блок может быть "короткоживущим" или "долгоживущим". Если в блоке все объекты уже не используются, то блок освобождается целиком. Подробнее про устройство GC1 можно посмотреть здесь.

Ресурсы

1. Мой код на гитхабе https://github.com/szelenin/kaggle/tree/master/billion-word-imputation

2. Описание с структуры Trie на википедии: http://en.wikipedia.org/wiki/Trie

3. Описание Trie с примерами : http://www.toptal.com/java/the-trie-a-neglected-data-structure

4. Как устроен GC1 : http://www.infoq.com/articles/G1-One-Garbage-Collector-To-Rule-Them-All
5. Kryo serialization framework : https://github.com/EsotericSoftware/kryo

Поиск среди миллиарда слов

Ничто так не настраивает на продуктивную работу, как день проведенный в совещаниях. Вот и я, после дня проведенного в бесконечных трындежах, решил сделать что-то полезное. Как только дома все уснули я решил покодить. Нашел интересный контест на Kaggle,  Billion Word imputation.

Суть задачи состоит в следующем:

Есть два файла. В первом - текст, состоящий большой кучи осмысленных предложений (на инглиш оф коз). Размер текстового файла примерно 3.86Гб и в нем находится примерно 1миллиард слов. Это тренировочный набор (training data).
Второй файл чуть поменьше (40мб). В нем из каждого предложения удалили по 1 слову.  Это тестовый набор (test data).
Задача: вставить пропущенное слово в тестовом наборе. Тексты никак друг с другом не связаны.

Как собираюсь решать

На тренировочных данных нужно построить модель, с помощью которой можно предсказать пропущенные слова в тестовом наборе. Какую модель будем строить?
Когда-то давно я прошел очень интересный курс по Natural Language Processing на Coursera от Columbia University. Основным элементом языковых моделей, которые мы рассматривали были так называемые N-Gram'ы. N-Gram - это последовательность N слов в предложении. Если N=1, то такую N-Gramm'у называют Unigram (т.к. одно слово), если 2-Bigram, 3-Trigrams и т.д.

Например, если разложить предложение "The dog likes the cat"  на N-Gramm'ы, то получится:

- Пять Unigram: The, dog, likes, the, cat

- 6 Bigram: * The, The dog, dog likes, likes the, the cat, cat _STOP_

- 6 Trigram: * * The, * The dog, The dog likes, dog likes the, likes the cat, the cat _STOP_

Здесь символ * и _STOP_ - это служебные символы, означающие начало и конец предложения.

Что можно сделать с этими N-Gramмами?

Можно посчитать вероятность, с которой встречается в тексте каждая N-Gram'ма. В простейщем случае (Unigram) вероятность слова w будет такой:

$$p(w)=\frac{count(w)}{N}$$

где N-общее количество слов в тексте, \(count(w)\) - сколько раз встречается слово w.

Например, в предложении "the dog likes the cat" \(p(the)=2/5\)

Если N > 1 (bigram, trigram и т.д.) то немного сложнее. Здесь мы должны считать условную вероятность \(p(w_n|w_{1},w_{2}...w_{n-1})\).  Это еще называют правдоподобием (likelihood). Т.е. это вероятность того, что слово  \(w_n\) встретится за словами \(w_{1} w_{2}...w_{n-2}w_{n-1}\).

В случае с биграммами мы будем "заглядывать" на одно слово назад, в случае с триграммами на 2 и т.д.
Вот как считаются вероятности для биграм
$$p(w_i|w_{i-1})=\frac{count(w_{i-1},w_i)}{count(w_{i-1})}$$
Где \(count(w_{i-1},w_i)\) - сколько раз встречаются вместе слова \(w_{i-1} w_i\), а \(count(w_{i-1})\) - частота появления слова \(w_{i-1}\)
Точно так же для триграм
$$p(w_i|w_{i-2},w_{i-1})=\frac{count(w_{i-2},w_{i-1},w_{i})}{count(w_{i-2},w_{i-1})}$$
Например, вероятность того, что likes встретится сразу за "the dog":
$$p(likes|the, dog)=\frac{count(the, dog, likes)}{count(the, dog)}$$

Как использовать расчитанные вероятности?

Допустим, что я как-то посчитал сколько раз встречается в тренировочном тексте все "the", "the dog", "the dog likes", "likes the cat", "cat _STOP_" и т.д. Как это можно использовать, чтобы найти пропущенное слово?

Поясню на примере.

Допустим, что в предложении "the dog likes the cat" удалили слово likes: "the dog likes the cat". Можно предположить, что likelihood для биграммы "dog the" будет очень маленьким, так же и для триграмм "the dog the" и "dog the cat". В идеале хотелось бы чтобы эти все 3 вероятности были бы нулевыми: 

\(p(the|dog)->{min}\)

\(p(the|the,dog)->{min}\)

\(p(cat|dog,the)->{min}\)

То есть нам надо пробежаться по предложению ("the dog the cat") и посчитать правдоподобия для всех bi-,tri-(возможно 4,5,6)-Gram в этом предложении. Если правдоподобие всех (или большинства) N-Gram минимально в одном и том же месте, то предполагаем, что в это место нужно вставить слово. 

Какое? тут уже надо искать слово, которое максимизирует правдоподобие (maximum likelihood) в заданном месте предложения. То есть если мы нашли, что слово удалили между "dog" и "the", то имеет смысл поискать что чаще всего встречалось после "the dog", "dog" и перед "the cat", "the". Это пока первоначальная гипотеза как можно найти слово, наверняка с реализацией она претерпит существенных изменений как это обычно бывает. 

Если есть мысли\предложения по поводу модели и реализации, то велкам. Про то, как я начал считать каунтеры расскажу в следующем посте. Там тоже интересно получилось :).

Ресурсы

Kaggle, Billion Word imputation contest

Курс Natural Language Processing на Coursera